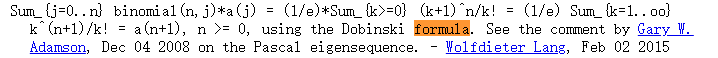五边形数(hard version) 根据等差数列求和,可以推知通项:
注意到 $n(3n-1) >2^{64}$,而 $\dfrac{n(3n-1)}2 < 2^{64}$,即直接计算会炸 ull,但是总答案不会, 而 $n,3n-1$ 必然一个奇数一个偶数。我们可以先选取其中的偶数将其计算 $\div 2$ 再乘以奇数,则不会爆 ull。当然用 i128 的话什么事情都没有。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;using ull = unsigned long long ;ull n, ans; signed main () cin >> n; if (n % 2 == 0 ) { ans = n / 2 * (3 * n - 1 ); } else { ans = (3 * n - 1 ) / 2 * n; } cout << ans; return 0 ; }
白茶与线程博弈(hard version) 设干扰线程删除了 $t$ 次时, 还剩下线程数 $m’$ 为:
设干扰线程最多删除 $t’$ 次,满足不等式:
记下取整表示为 $\lfloor x\rfloor$ ,如 $\lfloor 1.9\rfloor=1,\lfloor 2.0\rfloor=2$ 。解得:
那么前 $t’-1$ 次追踪线程都能追踪到 $30b$ 个踪迹; 第 $t’$ 次能追踪到 $m-7at-30b(t’-1)$ 个踪迹,故总追踪数 $f$ 为:
特别注意 $t’$ 为 $0$ 时,上式不成立,需要特判。这是因为 $t’=0$ 时上述式子的意义会变成干扰线程还没删除前追踪线程就追踪了,不符合题意。如果算到 $t’=0$ ,即:
说明第一次干扰就删完了,自然追踪不到,所以应该是输出 what a pity。
下面简要讨论该式子的数据范围。显然 $7a+30b,m+30b$ 在 long long 内。虽然中间变量 $t’=\lfloor\dfrac{m+30b}{7a+30b}\rfloor$ 的范围理论上也是 long long 的,但 $7at’$ 不可能会爆 long long。如果要爆 long long,则 $a$ 较大且 $t’$ 较大。设 $t’\ge c$,近似解得 $\dfrac{m+30b}{7a+30b}\ge c$ 即 $b\le\dfrac{m-7ac}{30(c-1)}$。设 $7at’$ 炸 long long,则有 $7at’\ge 2^{63}$,解得 $t’\ge \dfrac{2^{63}}{7a}=c$,代入得 $b\le \dfrac{(m-2^{63})a}{30(2^{63}-7a)}$。由于 $m\le 10^{16},a>0$,故分子 $(m-2^{63})a < 0$,且分母显然大于零,即 $b\le 0$,这与题给条件 $1\le b\le10^{16}$ 矛盾。因此,通过反证法严格证明出计算过程不会炸 long long。如果担心的话可以直接开 i128。或者可以用更简单的方法,即直接从现实意义出发,可知必然有 $f\ge 0$,即 $m\le 7at’$,故显然不会炸 long long。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;long long m, a, b, t, f;signed main () cin >> m >> a >> b; t = (m + 30 * b) / (7 * a + 30 * b); f = m - 7 * a * t; if (t && f >= m / 2 ) { cout << "I catch you, baicha" ; } else { cout << "what a pity" ; } return 0 ; }
高阶前缀和 设 $a=(1,1,\cdots)$,观察可得,有 $s_{j,i}$ 矩阵(这里设下标行 $j$ 从 $0$ 开始,列 $i$ 从 $0$ 开始):
抽象为 $s_{j,i}$ 表示从最左上角点 $(0,1)$ 出发,只能往左和往下走,共有多少种方案能走到 $(j,i)$。显然初始值是 $s_{0,1}=1$,且根据加法原理,有:$s_{j,i}=s_{j-1,i}+s_{j,i-1}$,可以发现该组合数学意义与前缀和数组算术等价。即问题暂时转化为问方案数。
显然,从 $(0,1)$ 走到 $(j,i)$ 共需要往下移动 $j$ 次,往左移动 $i-1$ 次,在这所有 $i+j-1$ 次移动里,分 $j$ 次往下,共有 $C_{i+j-1}^j$ 种方案。即:$a=(1,1,\cdots)$ 时,有:$s_{j,i}=C_{i+j-1}^j=C_{i+j-1}^{i-1}$。
现在推广到 $a=(a_1,a_2,\cdots, a_n)$,有:
换言之,现在抽象成了,可以从任一点 $(0,i)(i\le x)$ 出发,第一步只能往下走且方案数为 $a_i$,在这之后 只能往左和往下走,共有多少种方案能走到 $(j,i)(j\ge 1)$。显然,可以将其拆分为 $x$ 个子问题,即分别从 $(0,1),(0,2),\cdots,(0,x)$ 出发,走到 $(j-1,i)$ 的方案数,将这些方案数用加法原理加起来即可,有:
作偏移,有:
根据组合数学杨辉三角公式:$C_{n-1}^{r-1}+C_{n-1}^r=C_n^r$ 可知,$②+③=①$。由此,证明了该组合数学意义式子与题给前缀和式子等价。因此,可以用组合数学方法推导高阶前缀和。即所求为:
注意到 $y-1$ 很大,我们可以转化为求较小的 $C_{y+x-k-1}^{x-k}$,并且使用线性递推,即所求的从 $k=1$ 开始递增的组合数值分别是:
即每次让分子乘以多一个数,分母也改为下一个阶乘即可,可以降复杂度 $O(y)$ 为 $O(n)$。
设 $p=10^9+7$,可以 $O(n\log p)$ 或 $O(n)$(线性逆元)求出答案。前者参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mn = 1e5 + 10 , mod = 1e9 + 7 ;ll qpow (ll a, ll b = mod - 2 ) ll r = 1 ; for (; b; b >>= 1 ) { if (b & 1 ) { r = r * a % mod; } a = a * a % mod; } return r; } ll n, a[mn], x, y, t[mn], ans; signed main () cin.tie (0 )->ios::sync_with_stdio (false ); cin >> n >> x >> y; t[0 ] = 1 ; for (ll i = 1 , fm = 1 , fz = 1 , d = y; i <= n; ++i, ++d) { fz = fz * d % mod; fm = fm * i % mod; t[i] = fz * qpow (fm) % mod; } for (ll i = 1 ; i <= n; ++i) { cin >> a[i]; } for (ll i = x, j = 0 ; i >= 1 ; --i, ++j) { ans = (ans + t[j] * a[i]) % mod; } cout << ans; return 0 ; }
后者:(可以过自主思考)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mn = 1e5 + 10 , mod = 1e9 + 7 ;ll qpow (ll a, ll b = mod - 2 ) ll r = 1 ; for (; b; b >>= 1 ) { if (b & 1 ) { r = r * a % mod; } a = a * a % mod; } return r; } ll n, a[mn], x, y, t[mn], ans, fact[mn], inv[mn]; signed main () cin.tie (0 )->ios::sync_with_stdio (false ); cin >> n >> x >> y; fact[0 ] = inv[0 ] = 1 ; for (ll i = 1 ; i <= n; ++i) { fact[i] = fact[i - 1 ] * i % mod; } inv[n] = qpow (fact[n]); for (ll i = n - 1 ; i >= 1 ; --i) { inv[i] = inv[i + 1 ] * (i + 1 ) % mod; } t[0 ] = 1 ; for (ll i = 1 , fm = 1 , fz = 1 , d = y; i <= n; ++i, ++d) { fz = fz * d % mod; t[i] = fz * inv[i] % mod; } for (ll i = 1 ; i <= n; ++i) { cin >> a[i]; } for (ll i = x, j = 0 ; i >= 1 ; --i, ++j) { ans = (ans + t[j] * a[i]) % mod; } cout << ans; return 0 ; }
OEIS 设集合 $d_n=(b_1,\cdots, b_n),d_{n+1}=(b_1,\cdots, b_n,b_{n+1})$,考虑如何推导出 $b_{n+1}$ 的递推公式。
如果将最后一个元素 $b_{n+1}$ 单独划分到一类,则前 $n$ 个元素的划分数通过递归定义发现等于 $B_n$。
如果将最后一个元素与前面的任选一个元素划分到一类,有 $C_n^1$ 种选法,则剩下的 $n-1$ 个元素的划分数为 $B_{n-1}$,根据乘法原理,共有 $C_n^1B_{n-1}$ 种方案。
同理,将最后一个元素与前面的任选两个元素划分到一类有 $C_n^2$ 种选法,共有 $C_n^2B_{n-2}$ 种方案。
不断类推,设最后一个元素与前面 $k(0\le k\le n)$ 个元素划分到一类,有 $C_n^kB_{n-k}=C_n^{n-k}B_{n-k}$ 种方案。因此,递推公式为:
我们发现题目标题为 OEIS,而题目给出了前 $5$ 项,我们可以直接去搜索(可以打印 OEIS,赛时可以查询(数列按字典序排布,查起来不慢)),发现 $1,1,2,5,15$ 刚好是 A000110 即贝尔数。往下翻阅,能够查到递推公式:
这个公式表达的就是上文的公式,可以直接利用。
根据样例可知最大的 $B_{25}$ 不超过 long long。但计算组合数时,注意选择正确的方法,否则中间变量可能会爆 long long,用阶乘算式的话如果开 int128 则不会有事。推荐的方法是使用杨辉三角,能够保证不爆 long long。
杨辉三角求组合数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std;using ll = long long ;ll n; ll b[100 ], c[100 ][100 ]; signed main () cin >> n; for (ll i = 0 ; i <= n; ++i) { c[i][0 ] = 1 ; } for (ll i = 1 ; i <= n; ++i) { for (ll j = 1 ; j <= i; ++j) { c[i][j] = c[i - 1 ][j] + c[i - 1 ][j - 1 ]; } } b[0 ] = 1 ; for (ll i = 1 ; i <= n; ++i) { for (ll j = 0 ; j < i; ++j) { b[i] += c[i - 1 ][j] * b[j]; } } cout << b[n]; return 0 ; }
阶乘法:(这里化简了 $C_d^u=\dfrac{d!}{u!(d-u)!}=\dfrac{\prod_{i=d-u+1}^di}{u!}$)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;using ll = long long ;using i128 = __int128_t ;ll n; i128 b[100 ]; i128 c (ll df, ll uf) i128 r = 1 ; for (ll i = df; i >= df - uf + 1 ; --i) { r *= i; } for (ll i = 2 ; i <= uf; ++i) { r /= i; } return r; } signed main () cin >> n; b[0 ] = 1 ; for (ll i = 1 ; i <= n; ++i) { for (ll j = 0 ; j < i; ++j) { b[i] += c (i - 1 , j) * b[j]; } } cout << (ll)b[n]; return 0 ; }
自主思考:
若 $n\le 10^3$,无论用杨辉三角还是预处理阶乘+逆元都可以,加上取模公式即可。复杂度均为 $O(n^2)$ (后者可以线性逆元)。
若 $n\le 10^5$,根据贝尔数与第二类斯特林数性质,可知:$B_n=\sum_{k=0}^nS(n,k)$。
同一行第二类斯特林数的计算,可以用通项公式卷积或指数生成函数,具体参见 洛谷P5395 。将计算结果加起来就是 $B_n$。
换座位 这题即求长为 $n$ 的排列的错位数 $d_n$。
解法一:容斥原理推通项
设共 $n$ 人下有 $i$ 个位置的人没有换位,这 $i$ 个位置有 $C_n^i$ 种选择,则剩下 $n-i$ 个位置有 $C_{n-i}^{n-i}=1$ 种选择,而剩下的 $n-i$ 个位置都不一样,有 $(n-i)!$ 个组法,乘法原理合起来有 $C_n^i(n-i)!$。
设 $t$ 表示不满足题意的方案数,只要有人没换位都不满足,根据容斥原理有,$t=1$ 个位置的人没换位 $-2$ 个位置的人没换位 $+3$ 个位置的人没换位 $-\dots$,即:
则所求 $d_n$ 为总方案数 $n!$ 减去 $t$,即:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> using namespace std;using ll = long long ;ll n, f[30 ], d; signed main () cin >> n; f[0 ] = 1 ; for (ll i = 1 ; i <= n; ++i) { f[i] = f[i - 1 ] * i; } for (ll i = 0 , s = 1 ; i <= n; ++i, s *= -1 ) { d += f[n] / f[i] * s; } cout << d; return 0 ; }
解法二:递推公式
设已知 $d_i(i <n)$,要求 $d_n$。则:
若前面 $n-1$ 个人都换好座位了,有 $d_{n-1}$ 种方案,第 $n$ 个人还在原地,从前面的人里任选一个人有 $n-1$ 种选法,将选出的人与第 $n$ 个人交换座位,可以得到合法方案,乘法原理得 $(n-1)d_{n-1}$。
若前面 $n-1$ 个人里只有一个人还在原地,即剩下 $n-2$ 个人换好了,有 $d_{n-2}$ 种方案,选出这个在原地的人有 $n-1$ 种选法,将选出的人与第第 $n$ 个人交换座位,可以得到合法方案,乘法原理得 $(n-1)d_{n-2}$。
若前面的人有更多人在原地,且第 $n$ 个人也在原地,则找不到一次交换操作使得能够变成合法方案。因此,递推项只有两种可能,即:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <bits/stdc++.h> using namespace std;using ll = long long ;ll n, d[30 ] = {0 , 0 , 1 , 2 }; signed main () cin >> n; for (ll i = 4 ; i <= n; ++i) { d[i] = (i - 1 ) * (d[i - 1 ] + d[i - 2 ]); } cout << d[n]; return 0 ; }
自然数拆分 所求即分拆数 $p_n$。定义 $k$ 部分拆数 $p_{n,k}$ 表示把 $n$ 拆成 $k$ 个整数的方案,显然有 $p_n=\sum_{i=0}^np_{n,i}$。
而 $p_{n,k}$ 是下面方程的解的个数:
将每个 $r$ 用 $y=r+1$ 换元,有 $r\ge 1$ 即 $y\ge 0$ 代替,有:
转化为:
如果这里边的 $y$ 有 $j$ 个满足 $y \ge 1$,则等效于求子问题 $p_{n-k,j}$,因此,枚举所有 $j$,有:
更换变量,得:
作差,得:$p(n,k)-p(n-1,k-1)=p(n-k,k)$,因此,得到递推公式:
有初始值 $p_{0,0}=1$,因此本题得解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mn = 4e2 + 5 ;ll n, p[mn][mn], ans; signed main () cin >> n; p[0 ][0 ] = 1 ; for (ll i = 1 ; i <= n; ++i) { for (ll j = 0 ; j <= n; ++j) { if (i - j >= 0 ) { p[i][j] = p[i - j][j] + p[i - 1 ][j - 1 ]; } } } for (ll i = 0 ; i <= n; ++i) { ans += p[n][i]; } cout << ans; return 0 ; }
自主思考:可以使用五边形数定理求解。具体证明较复杂,感兴趣自行查。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mn = 1e5 + 10 , mod = 1e9 + 7 , i2 = (mod + 1 ) / 2 ;ll a[mn], p[mn], n; signed main () cin.tie (0 )->ios::sync_with_stdio (false ); cin >> n; p[0 ] = 1 ; for (ll i = 1 ; i <= n / 2 + 1 ; ++i) { a[2 * i - 1 ] = i * (3 * i - 1 ) % mod * i2 % mod; a[2 * i] = i * (3 * i + 1 ) % mod * i2 % mod; } for (ll i = 1 ; i <= n; ++i) { for (ll j = 1 ; a[j] <= i; ++j) { if (((j + 1 ) / 2 + 1 ) % 2 == 0 ) { p[i] = (p[i] + p[i - a[j]]) % mod; } else { p[i] = (p[i] - p[i - a[j]] + mod) % mod; } } } cout << p[n]; return 0 ; }
二分次数 可以证明,对于长为 $n=2^0+2^1+2^2+\cdots +2^p+c$ 的数组 $ASL$ 为:
即有 $2^0$ 个 $t(a_i)=1$,有 $2^1$ 个 $t(a_i)=2$,有 $2^2$ 个 $t(a_i)=3\cdots$,剩下不能凑够 $2^x$ 的有 $c$ 个。
注意到 $2^0+2^1+\cdots 2^p=2^{p+1}-1$,即对于给定的 $m,k$,有:
利用错位相减法,对 $c_n=(an+b)q^{n-1}=(1\cdot n+0)2^{n-1}$,其前 $n$ 项和为:
故 $S_n=(n-1)2^n+1$。其中 $n$ 对应 $p+1$。故所求为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mod = 1e9 + 7 ;ll qpow (ll a, ll b) ll r = 1 ; for (; b; b >>= 1 ) { if (b & 1 ) { r = r * a % mod; } a = a * a % mod; } return r; } ll m, k, ans; signed main () cin.tie (0 )->ios::sync_with_stdio (false ); cin >> m >> k; ans = ((m - 1 ) * qpow (2 , m) % mod + 1 + (m + 1 ) * (k + 1 ) % mod) % mod; cout << ans; return 0 ; }
FFT 可以发现,所有情况加起来,刚好凑齐所有排列。即所有排列可以分类塞到 sum 表达式里。故答案为 $n!$。(本题为2022省赛签到题)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <bits/stdc++.h> using namespace std;#define sc(x) scanf("%lld" , &x) typedef long long ll;ll mod = 998244353 , n, x = 1 ; signed main () sc (n); for (ll i = 2 ; i <= n; ++i) { x = x * i % mod; } printf ("%lld" , x); return 0 ; }
剪纸 题意即满足 $l+r$ 最小
可以发现,构造边长为斐波那契数列时,直观发现数量最多。所以找到最大不超 $n$ 的斐波那契 $f_i$ 并输出 $f_{i-1},f_i$ 即可。注意特判,$n=2$ 时不是 $1,2$ 因为两个正方形是相同的,是 $1,1$ (本题为2022省赛easy题)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;#define sc(x) scanf("%lld" , &x) typedef long long ll;ll n, a = 1 , b = 1 ; signed main () sc (n); if (n <= 2 ) { printf ("1 1" ); return 0 ; } while (b <= n) { ll t = a; a = b, b = t + a; } printf ("%lld %lld" , b - a, a); return 0 ; }
幂运算 先把底数为 $1$ (共 $n^2$ 种) 和底数不为 $1$ 且指数相等的情况(共 $n(n-1)$ 种)搞出来,其他情况都是不存在相等的。
有且仅有同底时能求出相等。同底的数可以互相分组,例如 $2,4,8,\cdots, 2^k$ 为一组,$3,9,\cdots,$ 为一组,$5,25,\cdots$ 为一组,$6,36,\cdots$ 为一组(组元素不能重复所以 $4$ 那里不能再开一组了)。
对于组内的元素,设最低底数为 $b$,任选两个组内元素 $b^u,b^v$,根据 $b^{ux}=b^{vy}$ 即 $ux=vy$ 有解。将方程化为最简形式即 $(u’,v’)=1$ 后,可以发现,在 $[1,n]$ 内有 $\lfloor\dfrac n{\max(u’,v’)}\rfloor$ 组解,即这些解是 $(v’,u’),(2v’,2u’),\cdots$。
问题即求:枚举每个组元素大于 $1$ 的组,任选两个指数 $u,v$ 组成 $A_n^2$ 个方程 $ux=vy$,求这些方程的小于 $n$ 的解数之和。显然,每组元素数目是 $\log n$ 级的,即枚举的复杂度为 $\log^2 n$,加上计算 $\gcd$ 的复杂度,共计 $O(\sqrt n\log^2 n\log\log n)\approx 1.4\times 10^8$(实际上远小于这个值),可以过题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <bits/stdc++.h> using namespace std;using ll = long long ;const ll mod = 1e9 + 7 ;ll n, ans; map<ll, bool > vis; signed main () cin >> n; ans = n * (2 * n - 1 ) % mod; for (ll i = 2 , p = 0 ; i * i <= n; ++i, p = 0 ) { if (vis[i]) { continue ; } for (ll j = i; j <= n; j *= i, ++p) { vis[j] = true ; } ll s = 0 ; for (ll u = 1 ; u <= p; ++u) { for (ll v = u + 1 ; v <= p; ++v) { ll g = __gcd(u, v); ll u2 = u / g, v2 = v / g; s += n / max (u2, v2); } } ans = (ans + 2 * s) % mod; } cout << ans; return 0 ; }
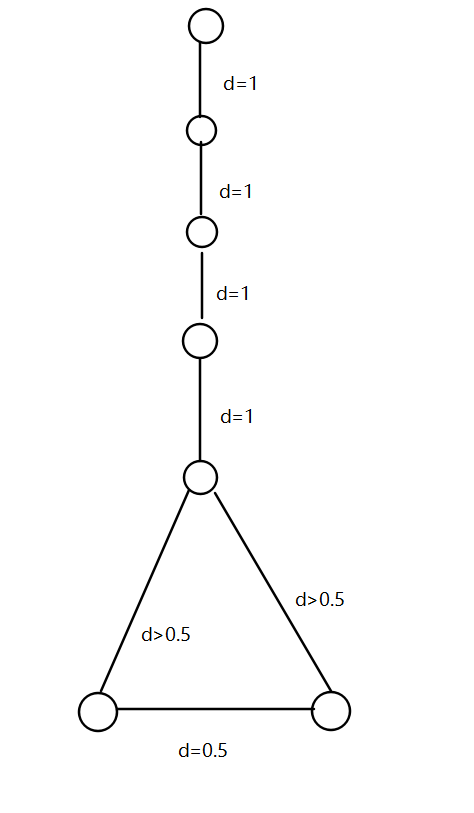
平面最近点对 分析代码特点,可知若我们在旋转后的坐标轴上绘制如下的点:
那么最下面的两个点间取得最小距离 $d=0.5$,但是根据排序结果,其中间被五个点挡住,所以对左下角点,只会求其与竖线上五个点的距离,求不到最小点。而之后求的每一个距离都必然大于 $0.5$。故该构造得解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <bits/stdc++.h> using namespace std;using ll = long long ;using db = double ;vector<pair<db, db>> v; signed main () db z = sin (-1 ), w = cos (-1 ); auto rot = [&](db x, db y) { db x_ = x * w - y * z; db y_ = x * z + y * w; return make_pair (x_ + 100 , y_ + 100 ); }; v.push_back (rot (0.75 , 0 )); v.push_back (rot (1.25 , 0 )); v.push_back (rot (1 , 1 )); v.push_back (rot (1 , 2 )); v.push_back (rot (1 , 3 )); v.push_back (rot (1 , 4 )); v.push_back (rot (1 , 5 )); printf ("%d\n" , v.size ()); for (auto pr : v) { printf ("%lf %lf\n" , pr.first, pr.second); } return 0 ; }
附:正确的平面最近点对解法(复杂度 $O(n\log n)$)如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 namespace solve_ac{ ll n; db ans = 1e18 ; const ll mn = 2e5 + 10 ; struct node { db x, y; bool operator <(const node &r) const { return x < r.x; } } p[mn]; void solve (ll lc, ll rc) { if (lc == rc) { return ; } ll cc = (lc + rc) >> 1 ; db cx = p[cc].x; solve (lc, cc), solve (cc + 1 , rc); inplace_merge (p + lc, p + cc + 1 , p + rc + 1 , [](const node &x, const node &y) { return x.y < y.y; }); vector<node> v; for (ll i = lc; i <= rc; ++i) { if (sqrt ((cx - p[i].x) * (cx - p[i].x)) <= ans) { v.emplace_back (p[i]); } } for (auto lf = v.begin (), rf = lf; lf != v.end (); lf++) { db sans = ans; while (rf != v.end () && rf->y <= lf->y + sans) { ++rf; } for (auto i = lf + 1 ; i != rf; ++i) { ans = min (ans, sqrt ((lf->x - i->x) * (lf->x - i->x) + (lf->y - i->y) * (lf->y - i->y))); } } } db getans (vector<pair<db, db>> &p0) { n = p0.size (); for (ll i = 1 ; i <= n; ++i) { p[i].x = p0[i - 1 ].first, p[i].y = p0[i - 1 ].second; } sort (p + 1 , p + 1 + n); solve (1 , n); return ans; } }