HyperLogLog 学习笔记

HyperLogLog

主要参考，附 C++ 个人实现

概率原理

近似快速计算一个集合有多少个不重元素。

设元素的哈希值有 $L$ 位，哈希值第一个 $1$ 出现的位置记作 $\rho(a)$，假设一定有 $1$ 出现，则所有哈希值的最高出现位置设为 $\rho_\max$，则可以近似估计不重元素数为 $n=2^{\rho_\max}$。

第一次出现的位置是第 $k$ 位，其概率等价于抛硬币伯努利过程，即 $P=\dfrac1{2^k}$，也就是说出现位置大于等于 $k$ 概率为 $\dfrac1{2^k}$，所以小于 $k$ 的概率是 $1-\dfrac1{2^k}$，所以 $n$ 个哈希值第一次出现 $1$ 的位都小于 $k$ 的概率为 $P_n(X < k)=(1-\dfrac1{2^k})^n$。都大于等于 $k$ 的概率为 $P_n(X\ge k)=\dfrac1{2^{kn}}$

则 $n$ 个哈希值至少有一个的位等于 $k$ 的概率是：上面的概率减去每次都不超过 $k-1$ 的概率，即：$P_n(X = k)=(1-\dfrac1{2^k})^n-(1-\dfrac1{2^{k-1}})^n$。

当 $n\ll 2^k$ 时，$P_n(X\ge k)\to 0$，而 $n\gg 2^k$ 时 $P_n(X < k)\to 0$。也就是说，哈希值个数 $n$ 远小于 $2^k$ 时，至少一个哈希值在 $k$ 位和之后出现 $1$ 几乎不可能；$n$ 远大于 $2^k$ 时，也几乎不可能在 $k$ 位之前都没出现过 $1$。与直观经验吻合。

设集合基数为 $n$，则 $2^{\rho_\max}$ 应当约等于 $n$，$\rho_\max$ 偏离很大的概率都约等于零。

也就是说，未知基数 $n$，可以通过观测最大的 $1$ 的位置 $\rho_\max$ 来预估 $n\approx 2^{\rho_\max}$。

平均数
后面 hyper log log 会用到。序列 $a$ 长度为 $n$：

Arithmetic Mean 算术平均 $\dfrac 1n\sum_{i=1}^n a_i$

对极端值敏感，极大或极小的值会对平均结果产生较大影响

Geometric Mean 几何平均 $\sqrt[n]{\prod_{i=1}^n a_i}$

广泛用于处理比率或增长率数据，如金融投资的年化回报率

当数据集包含的数值跨越多个量级时，几何平均数能有效平衡各数值的影响，避免极端值对结果的过大影响

Harmonic Mean 调和平均 $\dfrac n{\sum\dfrac1{a_i}}$

在处理速度、效率或其他倒数形式的数据时，调和平均数提供更为合适的平均值

合并不同大小的样本时计算平均值；对数据集中的小值较为敏感

LogLogCounting

LLC 论文 Loglog Counting of Large Cardinalities

定性地设计一个尽可能满足下面条件的哈希函数：

均匀（哈希结果理想上要均匀分布，但已经证明不可能通过一个哈希函数将一组不服从均匀分布的数据映射为绝对均匀分布，但是很多哈希函数可以生成几乎服从均匀分布的结果）(D. Knuth)
哈希碰撞概率忽略不计
哈希结果长度固定

将哈希值分成 $m=2^k$ 个桶，哈希值高 $k$ 位作为桶编号 $\in [0,m)$，剩下的位里找到第一个 $1$ 的位置。设桶 $i$ 的最大的位置是 $M_i$。

根据论文描述，原本是估计 $2^k$，但是不同 $k$ 差别太大了，所以用一个 $k$ 的平均值来代替，即取 $m$ 个桶的平均 $\rho_\max$ 即 $\dfrac 1m\sum_{i=1}^mM_i$ 来近似 $k$。则这几个桶的平均值来计数来估算 $n$：$\hat n=2^{\frac1m\sum_{i=o}^{m-1}M_i}$。

该表达式可以认为是幂 $\rho_\max$ 用了算术平均数，也可以认为是所有 $2^{M_i}$ 的几何平均数。

设哈希值长度为 $16$ 位，设 $m=2^5=32$，若有哈希值为：0001001010001010，则 00010 是桶编号剩下部分的第一个 $1$ 的位数为 $2$，所以该元素存桶就是把 $2$ 存进去。如果该桶只有一个元素，则 $M_2=2$。

该估计是有偏估计，转化为无偏估计：(详见论文)

$E=\alpha_mm2^{\frac1m\sum_{i=0}^{m-1}M_i}$

其中 $\alpha_m=\left(\Gamma(-\dfrac1m)\dfrac{1-2^{\frac 1m}}{\log 2}\right)^n,\Gamma(s)=\dfrac1s\int_0^{\infty}e^{-t}t^sdt$

论文给出结论，该观测值与实际值的标准误差为：$StdError(\dfrac{\hat n}n)\approx\dfrac{1.30}{\sqrt m}$

根据误差分析，如果想要误差在 $\epsilon$ 内，则 $m > (\dfrac{1.30}\epsilon)^2$

例如，最多可能有一亿类 $2^{27}$，设 $m=2^{10}$，则剩下 $27-10=17$ 位，也就是说 $M_i$ 的取值在 $[0,17]$，需要 $\lceil\log_2 17\rceil=5$ 位来存每个桶，即共 $5m$ 位，$5\times 1024\div 8=640 Byte$，只需要 $1KB$ 不到就可以近似存储一亿个类别。

因此，其空间复杂度为 $O(m\lceil\log_2((\log_2 k)-m)\rceil)$，其中 $m$ 是常数，$k$ 是值域，故复杂度为 $O(\log\log k)$。

HyperLogLog

HLLC 论文 HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm 在线演示 redis源码源码解析 (如哈希函数的设计可以参考源码)

改进一：调和平均数代替几何平均数。几何平均数对离群值（例如这里的 0）特别敏感，因此当存在离群值时，LLC 的偏差就会很大。n 较小时，可能存在较多空桶，而这些特殊的离群值强烈干扰了几何平均数的稳定性。

调和平均为 $\dfrac{m}{\sum_{i=0}^{m-1}\frac1{2^{M_i}}}$因此，估算公式变成了：$\hat n=\dfrac{\alpha_m m^2}{\sum_{i=0}^{m-1}2^{-M_i}}$。

其中，$\alpha_m=\left(m\int_0^m\log_2^m\dfrac{2+u}{1+u}du\right)^{-1}$

具体而言：(参考 vldbss-learned-cost-estimation-guoliangli，出处是 vldb2022的ss)

$\alpha_m=\begin{cases} 0.673,&m=16\\ 0.698,&m=32\\ 0.709,&m=64\\ \dfrac{0.7213}{1+\dfrac{1.079}m},&m\ge128 \end{cases}$

是无偏估计，渐近标准差为 $SE_{hllc}(\dfrac{\hat n}n)=\dfrac{1.04}{\sqrt m}$

分段修正建议：设估计值为 $E$

$E\le\dfrac52m$ 时，LC 估计(Linear Counting，线性复杂度，类似 bitmap) 参考

$\dfrac52m < E\le\dfrac1{30}2^{32}$ 时，HLLC 估计

$E > \dfrac1{30}2^{32}$ 时，$\hat n=-2^{32}\log(1-\dfrac E{2^{32}})$

基数估计的好处：可以并行化。因为可以很容易地合并结果。

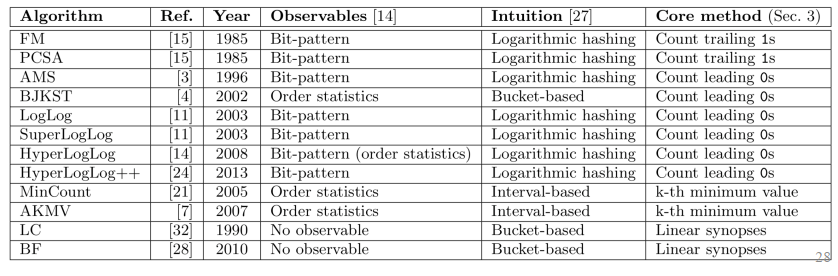
横向对比其他模型：（参考 vldbss-learned-cost-estimation-guoliangli）

FM, PCSA, AMS, BJKST, LogLog, SuperLogLog, HyperLogLog, HyperLogLog++, MinCount, AKMV, LC, BF

思想包括：计算尾 1/前导 0 / k-th 最小值 / 线性同义词(linear synoposes)

方法包括：基于区间、基于桶、对数哈希、顺序统计、位统计

C++ 个人实验实现：

实践表明：对小元素个数或小取值范围(没做哈希)，误差很大
如果取值范围很大(即假设进行了良好哈希)，且 n 较大(如 1e6 或以上)，准确率接近 1.04 之内
桶数多少与元素个数、取值范围有关，较小时(小于 1e5)干涉较大，较大时越多越准确

#include <bits/stdc++.h>
using namespace std;
using db = double;
struct HyperLogLog {
    int k, m; // 选择低 k 位作为桶编号，桶数为 m
    db a; // 修正因子
    vector<int> M; // 桶，没有做进一步位域空间优化/常数优化
    HyperLogLog(int k) : k(k), m(1<<k) {
        a = 0.7213 / (1 + 1.079 / m);
        M.resize(m, 0);
    }
    void insert(int x) {
        int i = x & ((1<<k)-1);
        M[i] = max(M[i], __builtin_ffs(x>>k));
    }
    int size() {
        db ans = a * m * m, s = 0;
        for(int i=0;i<m;++i) 
            s += 1.0 / (1LL<<M[i]);
        return round(ans / s);
    }
};

int main() {
    mt19937 mt;
    uniform_int_distribution<int> dist(1, 1e5); // 任意调整
    set<int> s;
    int n=2e6; // 任意调整
    HyperLogLog h(min(int(log2(n)),16)); // 任意调整
    for(int i=0;i<n;++i) {
        int x = dist(mt);
        h.insert(x);
        s.insert(x);
    }
    cout << s.size() << ' ' << h.size() << ' ' << (1.*h.size()/s.size()) << '\n'; // 任意调整
    return 0;
}

HyperLogLog++

论文 Hyperloglog in practice: Algorithmic engineering of a state of the art cardinality estimation algorithm 论文解读参考

改进：

将 32 位哈希函数优化为了 64 位哈希函数
将偏差纠正算法作修改，从 HllOrig 修改为 HllNoBias

新算法不管估算数据集大小有多大，都使用同样的内存空间(桶数目)

最后更新： 2024年06月13日 21:05

原始链接： https://lr580.github.io/2024/06/13/HyperLogLog/

lr580's 博客

建设期，不定期更新。

HyperLogLog 学习笔记

HyperLogLog

概率原理

平均数

LogLogCounting

HyperLogLog

HyperLogLog++